Tests

Hydrodynamical codes contain a wide selection of algorithms that must work in tandem to produce the correct results in real problems. Although we can test the individual lines of code to check that everything works independently, we must perform simulations of problems with known results to be confident that the code is working as expected. As with many other hydrodynamical codes, GANDALF contains a large test-suite of known problems to demonstrate that the code is functioning correctly

Hydrodynamical tests

Shocktube tests

Shocktube tests have been used to validate the accuracy of hydrodynamical codes for decades, in particular for capturing shocks and also for handling low-density rarefactions. We perform here two common tests; the adiabatic Sod test and the isothermal wall-shock test.

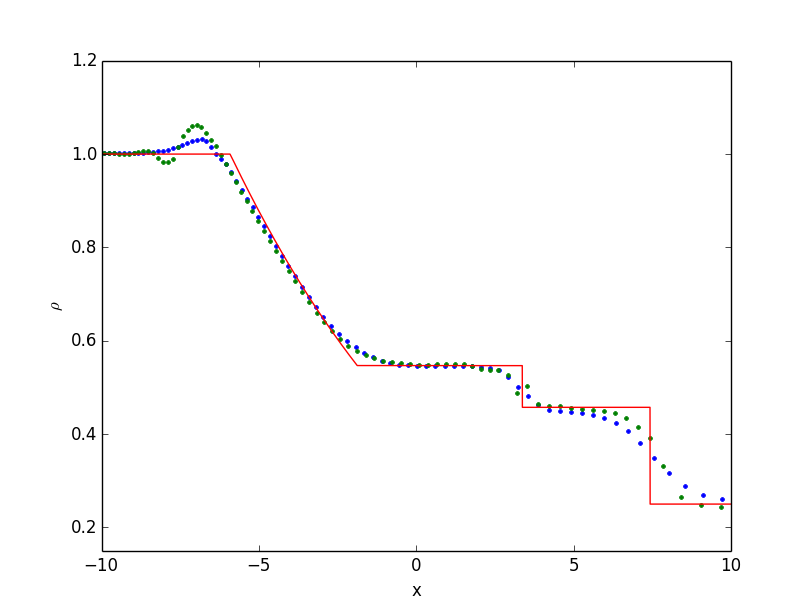
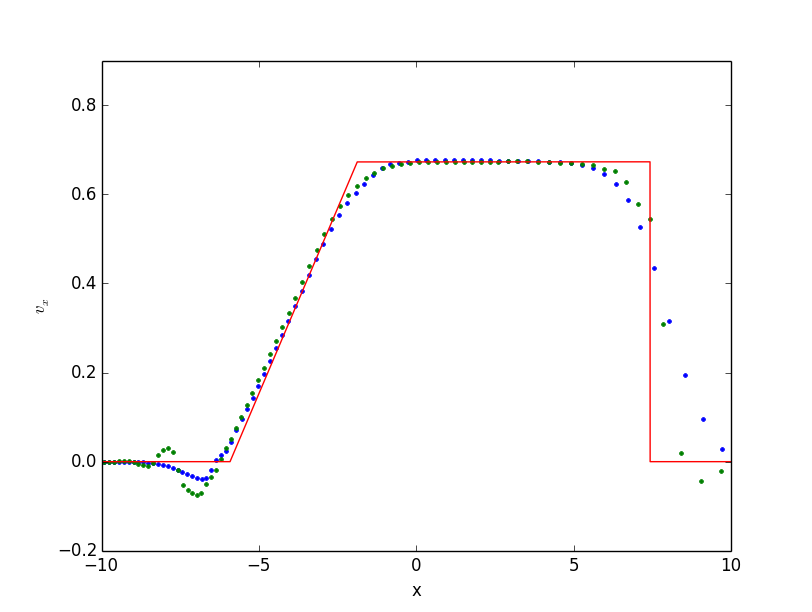
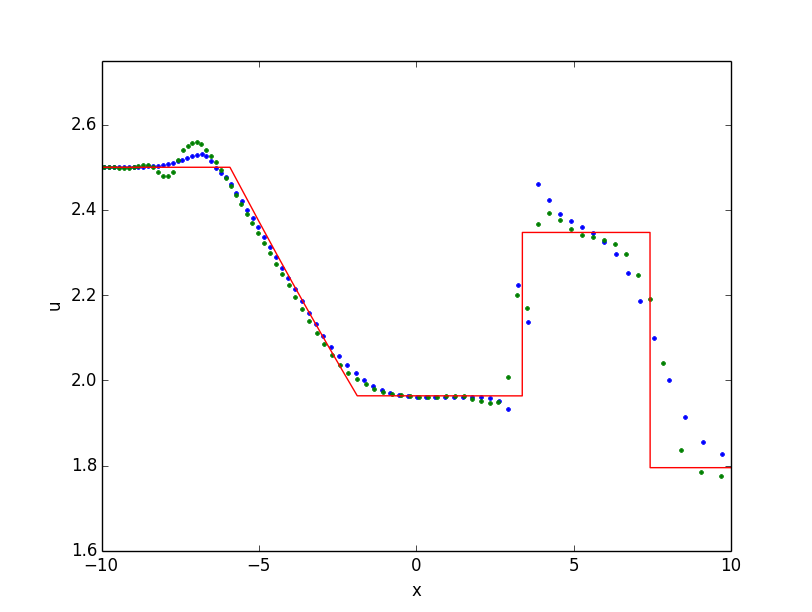
Blast-wave tests

Blast-waves are demanding tests of a code's ability to model strong explosions which generate a strong supersonic shock. Examples of such events in astrophysics include supernovae, high temperature winds and ionising radiation feedback from massive stars.

We perform here the standard Sedov blast-wave test (also known as the Sedov-Taylor blast-wave). The initial conditions are formally an infinitely extending cold uniform medium with a point explosion in the centre with total energy 1 (in dimensionless units). This explosion can be either in thermal energy or in radial kinetic energy. We simulate both cases here.

For SPH simulations, the initial conditions must be set-up more carefully since the smallest resolvable scale is the SPH smoothing length. Therefore to obtain acceptable results, the point explosion must be smoothed over all particles within a smoothing kernel.

Kelvin-Helmholtz instability

The Kelvin-Helmholtz instability is a hydrodynamical instability generated at the interface between two shearing fluids. The initial linear phase of the instability leads to the interface between the two fluids being displaced perpendicularly. As the displacement becomes larger, the instability becomes non-linear leading to the generation of vortices along the interface where the two fluids mix together. This problem became a subject of intense scrutiny in the literature following ???? where the effects causing mixing (or lack of mixing) were debated as being numerical in origin.

Gravitational tests

Gravitational freefall collapse

The simplest test of self-gravity is to model simple density profiles with known gravitational potentials and forces, such as a uniform density sphere or a polytrope. A uniform density sphere will undergo self-similar collapse under gravity in exactly one freefall time, and has a simple analytical form for both the time evolution of the density field and the gravitational field, both inside and outside the sphere.

We set up a uniform density sphere by relaxing a glass from SPH particles and 'cutting' out a spherical group of particles. We then (i) calculate the gravitational field at all points prior to the collapse calculation and compare to the analytical values, and (ii) follow the time-evolution of the sphere and follow its collapse down to just before it reaches very high/infinite densities.

Bondi accretion

Star formation simulations often use devices called 'sink particles' to model accretion onto a protostar accurately and efficiently. They allow simulations of self-gravitating collapse and accretion to proceed quickly while ignoring small-scale physics during the accretion process in favour of a sub-grid accretion model. To test whether the sink particles accrete correctly, we set-up a simple spherically symmetric steady-state accretion problem based on the Bondi accretion model.

The initial conditions are the standard sready-state Bondi accretion solution, derived by radially stretching a relaxed glass of SPH particles to the correct profile (details are described in ???). We then place sinks of sizes ????? at the centre. The simulation is run for ????, which corresponds to at least one sound crossing time of the sink particle.

Boss-Bodenheimer test

The Boss-Bodenheimer test is a standard benchmark that is often performed on self-gravitating hydrodynamical codes.

N-body tests

Few analytical N-body tests exist due to the non-linear/chaotic motion of self-gravitating point masses. We model the few standard benchmarks of N-body dynamics with the N-body integrators in GANDALF.

Binary orbit

The only stable analytical solution to the N-body problem is the 2-body problem involving a bound, stable orbit of one object around another. We follow the orbit of a binary star using the different integration schemes and measure the energy error for each case as a function of timestep.

Burrau test

The Burrau test is a standard benchmark test used in few-body codes. It follows the motion of 3 stars, initially set-up on a perfect triangle with zero-velocity. The system eventually evolves with one star being ejected in favour of the other two stars forming a tight binary.